RoPE:相对距离感知的秘密
1 背景与动机¶
Transformer 自注意力对序列顺序不敏感,必须显式注入位置信息。早期采用固定正弦/余弦绝对编码或可学习绝对嵌入,但它们难以表达相对距离且对长度泛化能力有限。相对位置编码(RPE)虽能部分缓解,但实现复杂、速度慢。RoPE 通过复数旋转一次性同时编码绝对和相对位置信息,为长上下文、大模型推理带来计算与泛化优势。
2 RoPE是什么¶
在大多数 LLM 代码与论文的实现里,RoPE 并不是“给词向量加一列坐标”的传统位置嵌入,而是在每个自注意力层内对 Query/Key 矩阵做一次按位置角度的旋转:输入 token 先进入词表查找得到\(h\),随后经线性投影分成\(q,k,v\),接着仅对\(q\)、\(k\)进行 apply_rotary_pos_emb,再进入点积‑Softmax 计算注意力权重。这一步发生在 Multi‑Head Attention 模块内部,与词嵌入矩阵本身(token embedding)解耦。
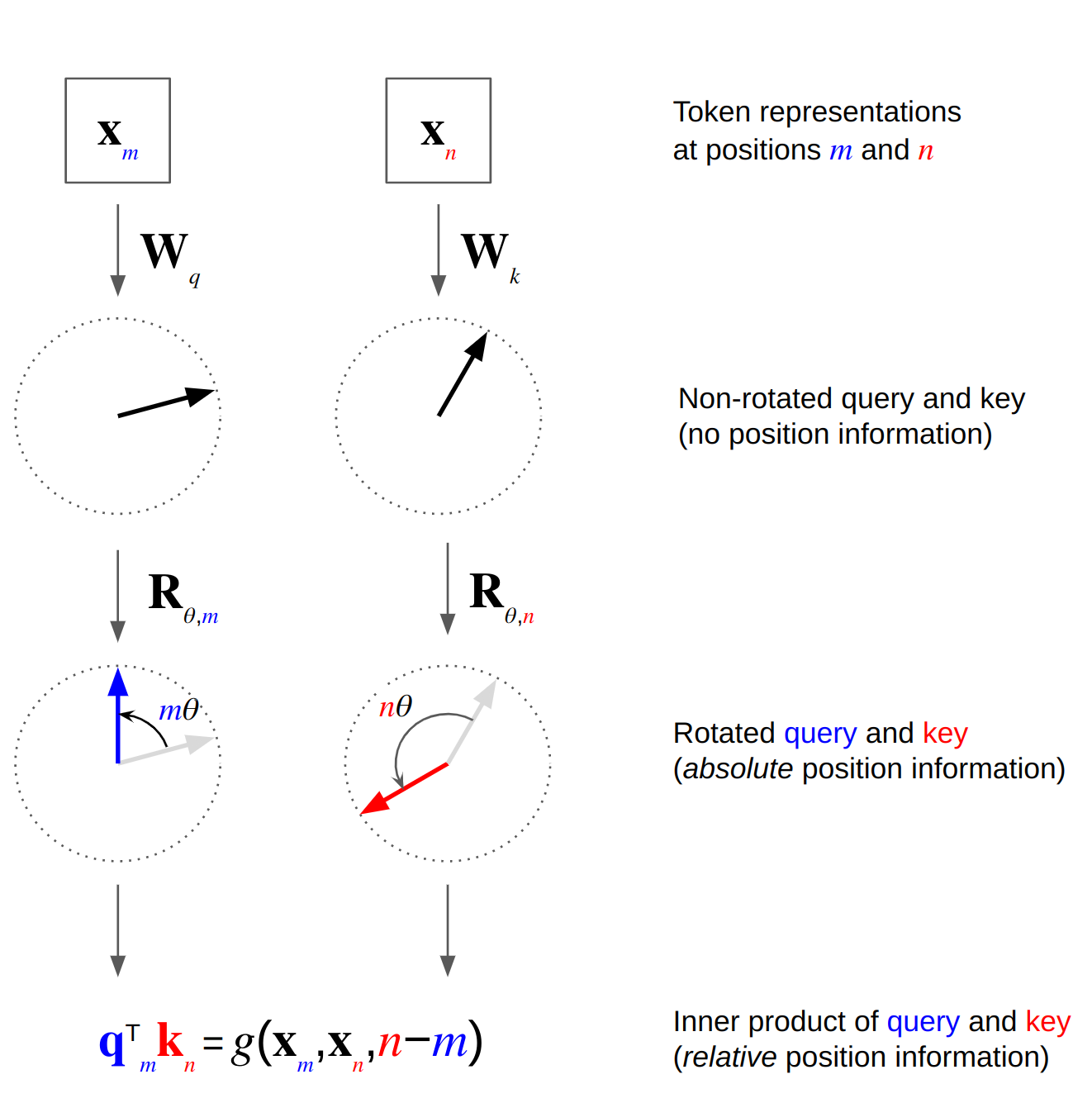
RoPE 最早由 RoFormer 提出,其核心思想是:把查询\(q\)和键\(k\)视为偶数/奇数交错的二维向量对\((x_{2i},x_{2i+1})\),对第\(p\)位应用同一角度\(\theta_p\)的旋转变换
\[R_{\theta_p}\begin{pmatrix}x_{2i},x_{2i+1}\end{pmatrix}= \begin{pmatrix}x_{2i}\cos\theta_p - x_{2i+1}\sin\theta_p \ x_{2i}\sin\theta_p + x_{2i+1}\cos\theta_p\end{pmatrix}\]
其中\(\theta_p = p/10000^{2i/d}\)与传统正弦编码同源。乘积\(q^\top k\)中旋转角度相减,自然产生相对位置偏差,因此自注意力仅依赖\(p_q-p_k\)。
性质
- 等变性:旋转矩阵保持范数不变,避免幅值爆炸。
- 相对距离单调衰减:内积随距离增大而余弦衰减。
- 无额外参数:与可学习绝对嵌入相比,参数为零,显存占用更低。
- 易于长文本插值/外推:通过伸缩\(\theta\)或插值,可把预训练 2 k → 128 k tokens。
真实代码示例
——StableLM‑Alpha 官方实现
cos, sin = rotary_emb(v, seq_len) # 预取旋转系数
q, k = apply_rotary_pos_emb(q, k, cos, sin, position_ids)
- 仅旋转 Q/K,不处理 V,是 LLaMA、StableLM、Phi‑3 等主流实现的共识
- 旋转操作位于注意力层里,因而 RoPE ≠ token embedding 的一部分;如果把 RoPE 提前到词嵌入阶段,相对位置信息在随后的线性投影中会被破坏,无法保证旋转角差等于相对距离
为什么选择在 Attention 内部旋转
- 相对位置信息天然保留\(q_i^\top k_j\)中角度差\(\theta_i-\theta_j\)只取决于\(i-j\),与绝对位置无关,实现了零参数的相对编码。
- 计算/显存零额外开销 旋转是逐元素乘加(或复数乘法),复杂度与原本点积相同;不需要为每个位置存表或向量。
- 推理阶段可缓存 cos/sin 相同长度只需一次预计算即可复用,在长上下文推理中比把位置向量加到\(h\)更节省带宽。
常见误区澄清
| 误解 | 事实与解释 |
|---|---|
| “RoPE 是另一种词嵌入” | 否。词嵌入负责语义,RoPE 仅在注意力求权重前对 \(q,k\)做旋转,从而把“位置信息”混入注意力分数,而非存进 token 向量。 |
| “RoPE 也要加到 Value” | 一般不加。\(v\)不参与 dot‑product,旋转对最终输出无用,反而浪费算力。部分实验对\(v\)旋转效果无显著提升。 |
| “换成 RoPE 只要改 Embedding 层” | 还需改 Attention。必须在所有自注意力层调用 apply_rotary_pos_emb;单独替换词嵌入层不会生效。 |
3 如何实现¶
3.1 PyTorch 伪代码¶
def apply_rope(x):
# x: (batch, seq, n_heads, head_dim)
x_even, x_odd = x[..., 0::2], x[..., 1::2]
pos = torch.arange(x.shape[1], device=x.device)
theta = pos[:, None] / 10000 ** (torch.arange(head_dim//2) / (head_dim//2))
sin, cos = theta.sin(), theta.cos()
x_rot = torch.stack([x_even*cos - x_odd*sin,
x_even*sin + x_odd*cos], dim=-1)
return x_rot.flatten(-2)
关键实现点:
- 先对维度做
reshape/view,保证偶数-奇数配对。 - 只对 Query 和 Key 旋转,Value 保持不变(LLaMA系做法)。
- 在推理阶段缓存
cosθ,sinθ以加速。
3.2 伸缩到长上下文¶
- Θ‑scaling:将\(\theta_p\)除以系数 \(s<1\)(NTK-aware scaling)以线性拉伸频率。
- 位置插值(PI):在更长序列上重新采样 \(\theta\),不需改模型权重;实验显示 RoPE‑PI 在 32 k+ 长度保持困惑度平稳。
- YaRN:微调少量 token,对 θ 动态缩放和分段 fine‑tune,可达 128 k 上下文且训练代价为前人 10%。