DeepSeekMath论文精读
0. 引言¶
- 定位:DeepSeekMath 是在代码基座上继续预训练的大规模数学模型,随后用指令微调与轻量强化学习进一步打磨。
- 关键抓手:
- 数据侧:用可迭代的网页挖掘与清洗流水线,构造约百亿量级的数学 token 继续预训练;
- 训练侧:在不引入价值网络的前提下,用 GRPO 进行强化学习,使策略分布更稳定。
- 结果:7B 量级模型在 GSM8K 与 MATH 等基准上取得强竞争力,在不开外部工具的设置下,报告显示 MATH Top-1 超过 50%,自一致性少样本采样进一步上升。
1. 为什么先从数据工程说起¶
多数“数学推理”工作的分水岭,不在“模型是否更深奥”,而在数据是否更对路。DeepSeekMath 的一个直接经验是:
- 从代码模型起步(更强的符号与语法感知),
- 用大规模网页数学文本做继续预训练(远大于常见教材与论文体量),
- 再用结构良好的指令数据做 SFT,
- 最后用不那么重的 RL 做抛光。
这条路线最大化利用了“数据分布与推理任务的一致性”,训练侧避免了“昂贵而脆弱的价值网络”,让小模型也能显出“稳定和复现”的质感。
2. DeepSeekMath 项目脉络¶
- 基座:以代码模型为起点的 7B。
- 继续预训练:以网页数学语料为主,规模约百亿 token 级。
- SFT:约 70 多万条中英数学指令数据,覆盖 CoT、PoT、工具增强等格式。
- RL:采用 GRPO(Group Relative Policy Optimization),通过组内相对奖励估计优势,不再训练价值网络;在损失项里直接加入与参考策略的 KL 正则。
3. 数据处理 pipeline¶
下面这条流水线不是“唯一正确”,但它解释了 DeepSeekMath 在“规模、纯度、结构化程度”上的做法,且便于复用到其他专业领域。
3.1 端到端视图¶
3.1.1. 候选发现¶
- 用关键词、正则与轻量分类器(如 fastText)在 Common Crawl 这类大库里做初筛,给每个页面一个“数学相关度”打分。
- 以“样本高分页面的域名、目录模式”为线索,做域级与路径级扩张,比如持续抓取
math.*、/problem/、/solution/一类高产路径。
3.1.2. 迭代回采¶
- 统计正例集中出现频率高的域名和 URL 模式,建立“可靠源清单”。
- 基于“域名得分 + 路径模板得分 + 页面得分”做加权回采,形成“数据-模式-回采”的闭环。
3.1.3. 内容抽取与结构化¶
- HTML 去模板、去导航、去广告,保留正文与代码块;
- 识别题目、步骤、结论等结构片段,尽量抽取“题面-推理-答案”三段式;
- 识别公式块与行内公式,将其与上下文绑定,避免丢失语义邻域。
3.1.4. 清洗与去污¶
- 语言筛选(优先中英),长度与稠密度阈值过滤;
- URL 归一化与去跟踪参数,精确去重(hash)与近重复去重(SimHash 或 MinHash);
- 对基准集做 n-gram 层面的泄漏去重(如与 GSM8K、MATH 等形成黑名单 n-gram),防止训练-评测穿模。
3.1.5. 质量评估与抽样¶
- 训练轻量质量分类器,特征包含:数学密度、代码密度、困惑度、结构完整性等;
- 分位抽样,保证不同来源、不同子领域都能被覆盖;
- 对噪声较多的子域(例如几何与图形)单独加权补齐。
3.1.6. 数据混合策略¶
- 继续预训练阶段维持一个多元混合:数学网页为主,配比加入代码、学术论文、自然语言泛化文本等,以减缓“能力遗忘”;
- 指令阶段统一格式(见 3.3),兼顾 CoT、PoT 与工具格式,形成面向推理的高信度标注集。
3.1.7. 标注一致化与审计¶
- 统一标注模板,保证“题面-推理-答案”的列对齐;
- 对易错题型设立审计样本池,训练中周期性抽检,形成“数据-训练-评测-返修”的闭环。
3.2 两个关键子模块¶
A. 数学性判别器(Mathness Scorer)
- 输入特征:公式密度、数学术语词表匹配、代码与数字占比、句法复杂度、困惑度分段等。
- 目标:把“教程类”“题解类”“学术类”“论坛问答”等高价值页面打到高分,把“目录页”“聚合页”“广告页”打到低分。
- 用途:排序与阈值,指导回采与抽样。
B. 近重复去重(Near-Dup)
- URL 层面:归一化去参;
- 文本层面:文段级分块,句子级去重,SimHash 或 MinHash 检测 80% 以上相似度的近重复;
- 评测泄漏守门:维持一个“评测 n-gram 黑名单”,训练集中若出现这些 n-gram 序列,直接剔除或替换。
3.3 指令数据的统一格式¶
建议在 SFT 阶段统一到如下三段式模板,便于后续 RL 与评测:
{
"question": "题面(可含必要上下文与约束)",
"reasoning": "逐步推理过程(CoT 或 PoT:可包含运行日志或中间变量)",
"answer": "最终答案(严格对齐评测口径)",
"meta": { "lang": "zh|en", "domain": "algebra|geometry|number_theory|..." }
}
- CoT:偏文字推演;
- PoT:偏程序化推导(例如 Python 小段落),注意把“计算过程”与“口径一致的最终答案”明确区分;
- 工具格式:再加一个
tool_calls字段,记录允许外部工具时的调用序列与返回值。
4. 训练工艺:从继续预训练到 SFT¶
- 继续预训练
- 数据以数学网页为主,穿插一定比例代码、论文与通用文本;
- 目标是把“数学语义、符号习惯、题解文体”内化到基座里;
- 训练曲线关注困惑度、字表覆盖度、公式还原率、结构稳定性等指标。
- SFT
- 用统一格式的指令数据做监督微调;
- 混合 CoT 与 PoT,PoT 关注“稳态可执行推导”,CoT 关注“可读与可审计的逻辑链”;
- 对齐评测口径:保证
answer字段与基准评测的判分规则完全一致(大小写、空格、单位、分数与小数等)。
5. GRPO:轻量但有效的强化学习¶
动机:PPO 虽然常用,但价值网络既吃显存又容易不稳,尤其在“奖励只在结尾给分”的数学任务上,token 级价值学习很难。
GRPO 的取舍:
- 不训练价值网络,直接在同题多解的组内做相对比较,以组内均值作为基线,构造优势;
- KL 正则直接放到损失项里,约束新旧策略的偏移幅度;
- 仍保持 PPO 的裁剪结构,让更新不过猛。
一步到位的训练框:
- 旧策略对同一题目采样 G 条候选;
- 用自动判分、格式校验或弱标签对候选给分;
- 计算组内相对奖励,得到每个 token 的优势估计;
- 新策略做裁剪后的策略梯度更新,同时加上对参考策略的 KL 正则;
- 监控两个指标:
- Pass@K(至少一条正确)
- Maj@K(多数表决正确)
经验证,RL 更明显改善 Maj@K,说明“正确解”从小概率尾部被挪到了主模态。
超参提示:
- 组大小 G 建议中等(例如 4 到 8),过小方差大,过大会拖慢;
- KL 系数从小到中,配合温度与长度惩罚调优;
- 对“有明确答案”的题目更稳,对“开放式”或“几何绘图”类要小心噪声奖励。
6. 实验结果¶
6.1 数据流水线带来了什么¶
6.1.1 语料对比:DeepSeekMath Corpus vs 其他数学语料(1.3B模型,few-shot CoT)¶
| 语料 | 规模 | GSM8K | MATH | MMLU STEM | CMATH |
|---|---|---|---|---|---|
| 无数学训练 | N A | 2.9 | 3.0 | 19.5 | 12.3 |
| MathPile | 8.9B | 2.7 | 3.3 | 15.7 | 1.2 |
| Proof-Pile-2 | 51.9B | 14.3 | 11.2 | 29.2 | 19.9 |
| DeepSeekMath Corpus | 120.2B | 23.8 | 13.6 | 33.1 | 41.5 |
可以看到,仅靠更好的网页数学语料,1.3B模型在GSM8K和CMATH上大幅领先同类语料,同时在MATH与MMLU STEM上也更稳。更重要的是,学习曲线随token持续上升,未过早“平台化”。
6.1.2 抓取与去污的关键动作¶
- fastText召回高分页面,按域与路径模式迭代回采,四轮后得到约35.5M页面、120B token;对评测集做n-gram去污染。
- 直接结论:网页挖掘是数学文本的“富矿”,规模与质量上均优于小体量的纯学术语料;后文也将看到,单用arXiv并不理想。
6.2 继续预训练:代码基座 + 混合配比的收益¶
7B Base与同类基座对比(few-shot CoT,不开工具)
| 模型 | 尺寸 | GSM8K | MATH | SAT | MMLU STEM | CMATH |
|---|---|---|---|---|---|---|
| Mistral | 7B | 40.3 | 14.3 | 71.9 | 51.1 | 44.9 |
| Llemma | 34B | 54.0 | 25.3 | 71.9 | 52.9 | 56.1 |
| Minerva | 540B | 58.8 | 33.6 | 63.9 | ||
| DeepSeekMath-Base | 7B | 64.2 | 36.2 | 84.4 | 56.5 | 71.7 |
同为开源基座,DeepSeekMath-Base 7B在所有基准上都处于第一梯队,尤其MATH 36.2%显著超过同尺寸与更大尺寸的开源基座,接近Minerva大模型段位。其数据配比里仍保留20%代码与10%通用文本,有助于稳住通用能力。
6.3 指令微调:把“题面-推理-答案”统一起来¶
- 约776K条中英数学指令,覆盖CoT、PoT与工具集成格式。以该数据在Base上做SFT,得到的Instruct 7B在不开工具时:GSM8K 82.9%,MATH 46.8%;允许工具时,MATH+Python 57.4%。
6.4 GRPO强化学习:小改造,实打实的增益¶
从Instruct到RL的增量
| 模型 | GSM8K | MATH | MGSM-zh | CMATH |
|---|---|---|---|---|
| DeepSeekMath-Instruct 7B | 82.9 | 46.8 | 73.2 | 84.6 |
| DeepSeekMath-RL 7B | 88.2 | 51.7 | 79.6 | 88.8 |
允许工具时:GSM8K+Python从83.7%到86.7%,MATH+Python从57.4%到58.8%,中文两项也同步抬升。
RL前后对比显示,Maj@K显著提升,而Pass@K近似持平。这说明RL让正确解从“尾部小概率”迁移到“主模态”,减少采样数也能稳定拿到对。对工程落地,这等价于更省采样、更好复现。
6.5 代码训练为什么要保留:程序辅助推理和通用能力都受益¶
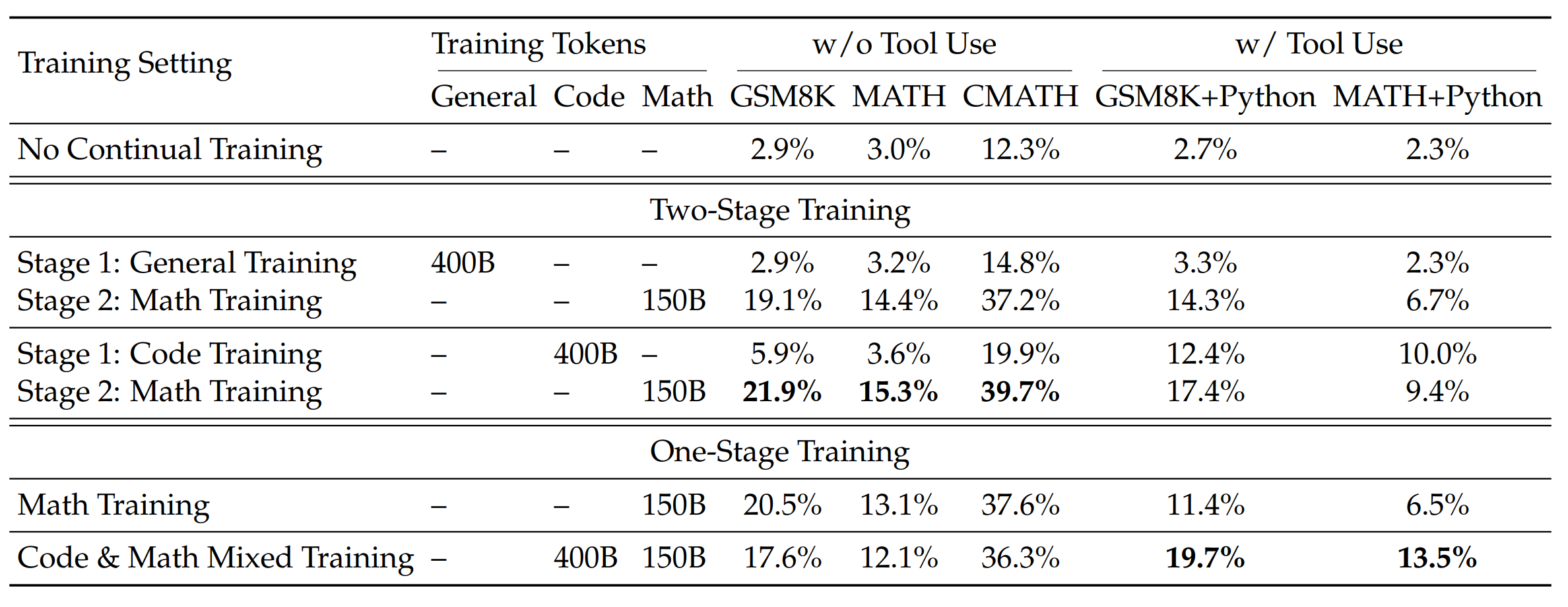
6.5.1 两阶段与一阶段的实测(1.3B)¶
先做代码再做数学,PoT类任务的能力更强,且二阶段后的整体表现更好。代码数据混合训练,对于工具使用效果更佳。
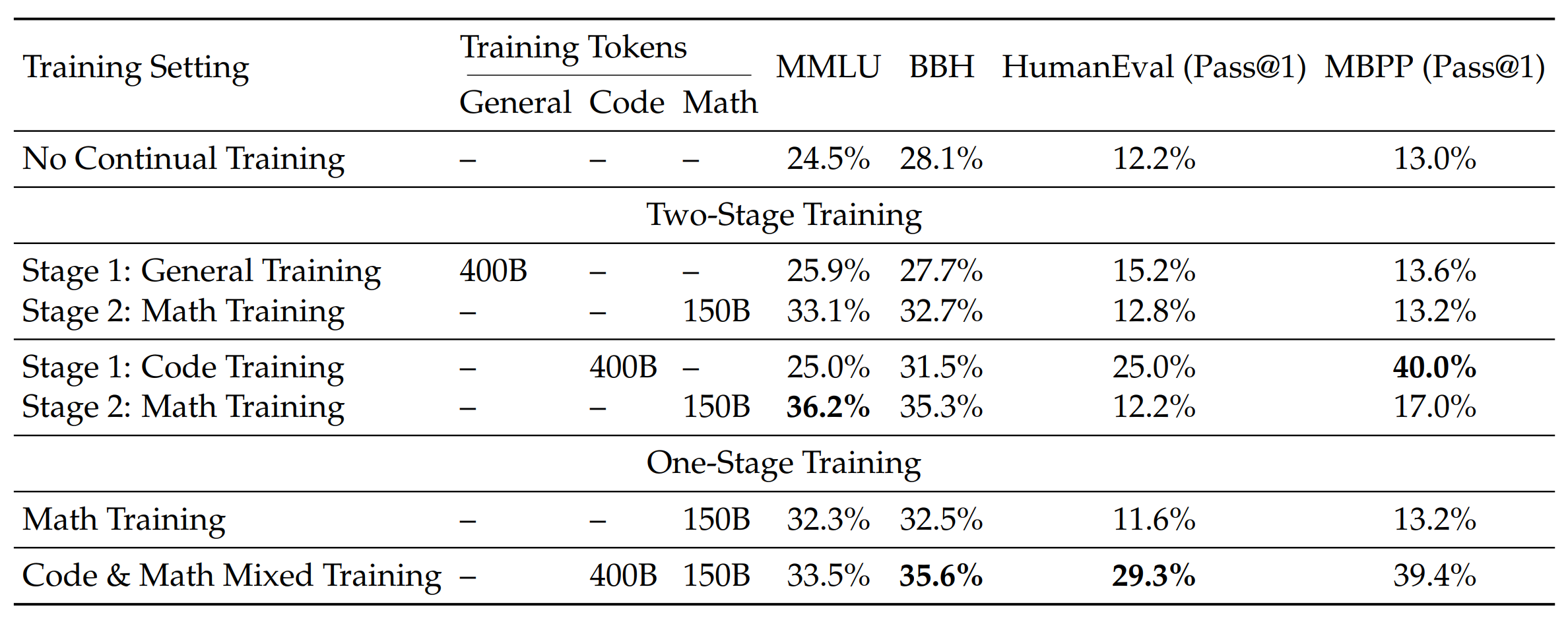
6.5.2 代码与数学混合的一阶段训练还能守住编程能力(1.3B)¶
混合一阶段不但保持了推理与通用能力,还显著提高HumanEval和MBPP,缓解二阶段后的“灾难性遗忘”。对实务来说,这样的配比能让系统在数学与代码双轨任务上更稳。
6.6 关于arXiv:在本项设置下收益不明显¶
- 在1.3B与7B上做过多组对比,仅用arXiv系语料进行数学训练,对GSM8K、MATH、MMLU STEM乃至miniF2F并无收益,甚至会退化。下表节选两组结果:
- 7B基座数学训练于MathPile或ArXiv-RedPajama后,GSM8K和MATH均低于无数学训练的同尺寸基座某些项;
- miniF2F上,arXiv训练后的valid与test也显著低于无数学训练。
注:作者也强调这一结论有范围条件,未来还需在更大模型或更细分任务上再次验证。
6.7 模块作用与数据支撑小结¶
- 网页数学语料:把1.3B从GSM8K 14.3%左右提升到23.8%,CMATH从19.9%到41.5%,并延缓“平台期”。这证明迭代抓取与去污确实在质量与规模上更优。
- 代码初始化与保留:7B Base在MATH 36.2%且MMLU STEM 56.5%,说明代码分布对数学与通用推理都有正向作用;在1.3B上,代码→数学的两阶段和代码+数学混合均能提升PoT与编程类基准。
- SFT统一格式:Instruct 7B不开工具已到MATH 46.8%,为RL提供了稳定起点。
- GRPO强化学习:在不引入价值网络的前提下,把MATH再抬5个点到51.7%,且GSM8K到88.2%;核心收益是让“正确解”更集中,Maj@K显著上升。
- 剔除潜在无效数据源:在本设置下,单用arXiv难以提升数学推理,资源更应倾斜到网页挖掘与高质结构化题解。
实施建议
- 先把数学网页“挖干净”:做一个领域判别器先跑通闭环;从域名和路径模板扩张;严格n-gram去污染。
- 保留代码与通用文本的占比:继续预训练阶段维持混合,避免数学强化后通用与编程能力塌陷。
- SFT统一模板,口径一致:题面-推理-答案的三段式有利于后续RL与评测。
- RL优先用GRPO:组大小4到8,温和KL,先看Maj@K曲线是否上扬;必要时做两轮迭代RL。
7. 总结与思考¶
DeepSeekMath 是一套完整的“工学方法论”:
- 用迭代式数据挖掘把“数学文本的真实分布”搬进模型;
- 先做一个“领域相关度”判别器,尽快让抓取闭环跑起来;
- 极度重视去重与泄漏守门,优先构建评测 n-gram 黑名单;
- 对薄弱子域(如几何)单独补齐来源和标注;
- 混合保留一部分代码和通用文本,防止能力塌陷。
- 用统一的指令格式提升可训练性与可评测性;
- 继续预训练阶段关注“结构稳定性”与“公式还原”,多做灰度评估;
- SFT 统一模板,严格对齐评测口径;
- 用轻量 RL 做最后的分布修正,让正确解更“可复现”。
- RL 起步用 GRPO,G 取 4 到 8,KL 从小到中递增,重点盯 Maj@K 与解的多样性。
- 除了标准分数,务必看两件事:
- 正确解是否集中在少量模式(多样性下降的风险);
- 错误是否集中在某些子域(面向数据回补与训练再平衡)。
这四个抓手在其他领域依然成立:先把数据分布找对,再把训练工艺走顺,然后用小而稳的 RL 优化,最后评价回溯。
参考
- DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models, arXiv:2402.03300